引言

为了得更好更优越的远行性能与减少操所需要的时间，才廷生出一种，优越的查找算法—–二分查找。
二分查找即一种算法，接受输入有序元素列表和所找元素，若所找无素包含在有序列表中，即返回位置，反之则返回null

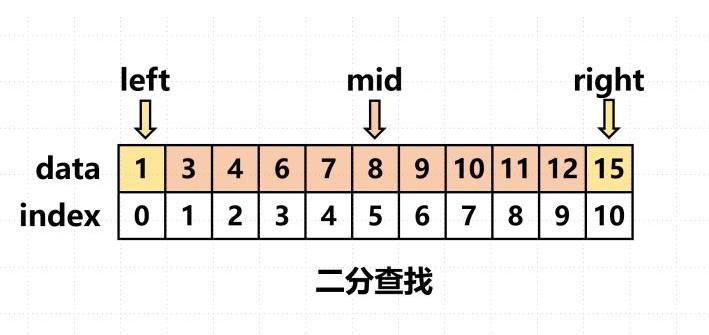
例如你在一家网站平台登录，在输入用名时，要在服务器查找相应信息、如果这家网站用户量10万，需在10万中查找，可根据用户名首字母排序，从26字母中间查找开始，相比从头开始，要省去一半的查找量，有一组有序数列包含100个 元素，

二分查找与简单查找

我想查找1~100个数字中任意一个元素数字所在位置，现有两种算法，一种简单查找，一种即二分查找，为了更深入理解二分查找的原理，在此作以
区别

首先:简单查找，

简单查找，便是从头到尾依次，为所查找元素/依次进行查找。

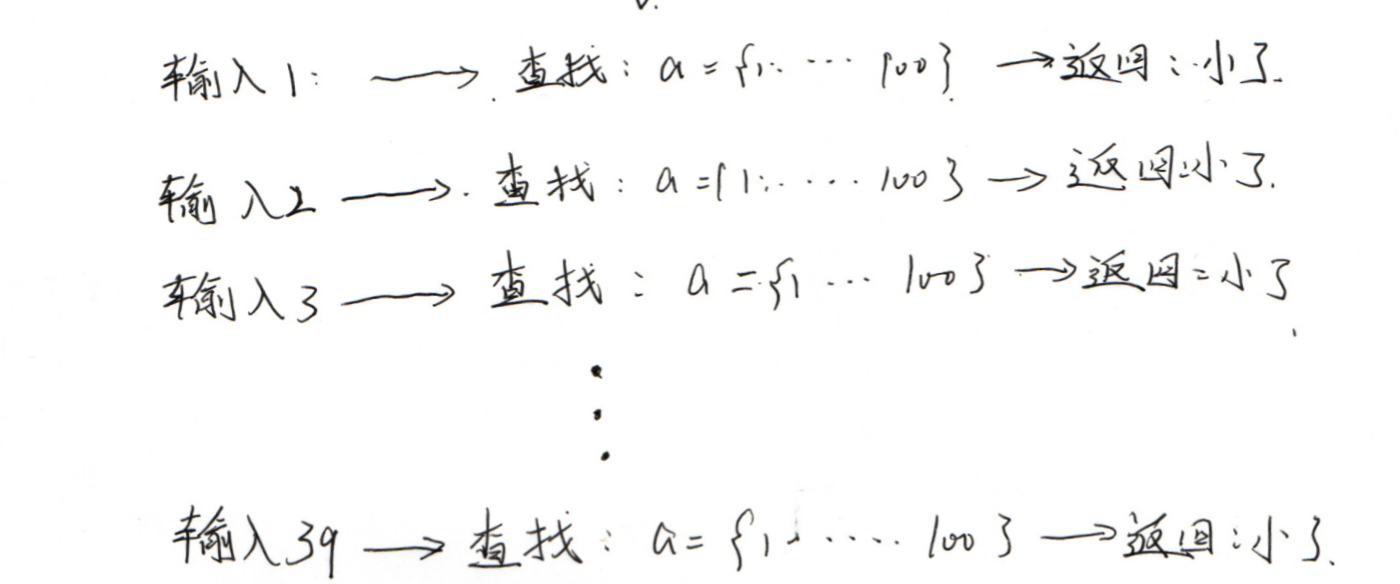
就这样简单查找需要遍历有序列表中每一个无素、如上，便需进行100 次查找操作才有可能找到所需元素位置，假如一个有序列表中含有10万个元素，仅设每次查找操作1毫秒，全部下来也需10万毫秒，甚比几天，显然不太现实。

其次：二分查找，

二分查找便是从中间开始查找，将一个有序数列从中间分成两个区间通过比较找到所查元素所在区间，依次往复便可找到该元素，这样每次将所找区间分为二分之一便提高了效率，缩短查找时间。
Ps:类例于用二分法来解方程求近似解，但有些异同。

在区间[1~100]之内。不论查询哪一数字，仅在7步操作之内便可，相比简单算法舍去了许多不必查找的区间，因此节省大量服务器资源，时间，提升性能

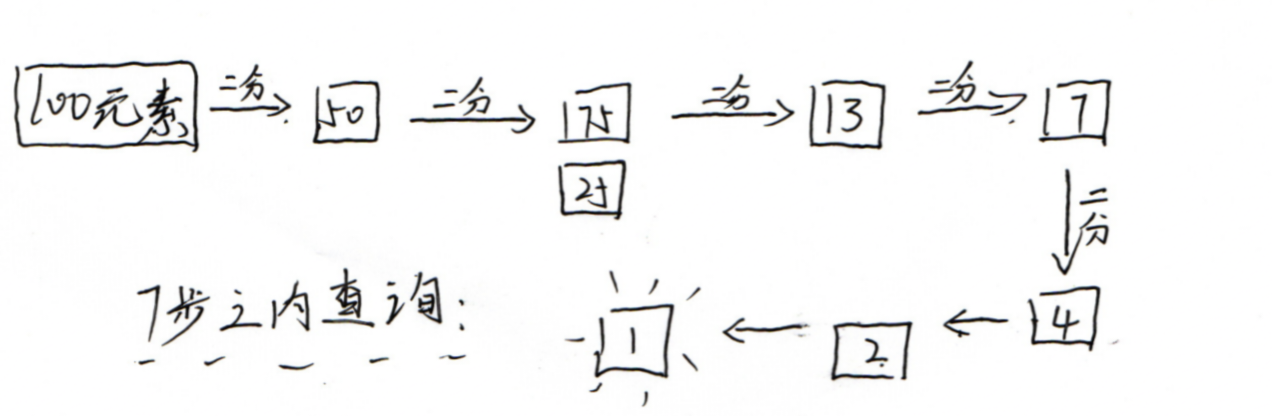
假设查询一本含240000 个单词的字典，用上
图二分查询操作流程图便可知仅需18步， 每次排除一半直至
剩下一个单词。

总结

规律:依据许多实例对于n个元素的有序列表，仅需log2ⁿ次
操作而简单操作则需n步。
二分查找–案例
案例：函数binary_search接收一个"有序数组"和"一个元素"。
如果,指定的元素包含在数组中，这个函数将返回其位置。

案例

python案例

def binary_search(list, num):                          
    low = 0                         # 最小索引
    high = len(list) - 1            # 最大索引

    while low <= high:
        mid = int((low + high) / 2)  # 向0取整，中间值的索引
        guess = list[mid]            # 猜中间值

        if guess == num:             # 找到了元素
            return ('got %d in index of %d') % (num, mid)

        if guess < num:              # 猜小了，增加最小索引
            low = mid + 1
        else:
            high = mid - 1           # 猜大了，缩小最大索引

    return None

my_list = [1,3,5,7,9]
find_num = 3
print(binary_search(my_list,find_num))
find_num1 = 4
print(binary_search(my_list,find_num1))