绝对值相关问题-初升高衔接
首先进行一下初中知识回忆,对高中的知识理解有帮助
初中知识回忆
绝对值的代数意义:正数的绝对值是它本身,0的绝对值是0,
即|a|=a(a>0)|a|=0(a=0)|a|=-a(a<0)
绝对值的几何意义:即一个数的绝对值到数轴上表示它到原点的距离,
两点间差:|a-b|即表示a到b在数轴上的距离.
绝对值的性质性质:
(1)|al≥0 |al≥a |al≥-a
(2)若|al=|bl 则b=a或 b=-a.
(3).若a>b>0时.则|a|>|bl.
(4)若a<b<0时则.lal<lbl.
(5)lal>lbl 则a²=b²
(6)|a|²=l²l=a² 和 a×b=lallbl
注意1.由lal>lbl不能得出a>b.因取出绝对值,后无法判断a,b取前的正负情况
2.去绝对值符号的方法有两种后面会讲到,平方法和零点分段法
高中绝对值知识衔接
导言:
高中的绝对值与初中的绝对值相对较为复杂,初中时主要用定义法判断数字或代数式正负的情况而高中需去掉绝对值符号的代数式,不仅用定义法,且有分类讨论法(又称零点分段法)去绝对值符号关键在于判断代数式的正负情况围绕这一核心要点进行下例研究:①对含绝对值的方程求解.②对含有绝对值的函数化简.③对含绝对值的式进行求解④含绝对值的式子化简.
含有绝对值的方程求解.
例如:|3x-2|=x
①.去绝对值符号:3x-2=x 3x-2=-x(根据|a|=±a).
②分别解出方程解:3x-2=x 3x-2=-x
③写下所求解. x=1或x=2
绝对值
对含有绝对值的方程求解只用了定义法将绝对值a进行正负解答罢
对含绝对值的函数化简
对含有绝对值的函数化简时主要运用了区间讨论的方法(又称零点分段法)进行化简,去掉绝对值符号。当函数为单个变量时可用定义法,含绝对值的函数,首先绝对值去号后的数值一定是正数,因此.函数也一定是正的。.
在对函数详解之前我们先了解一下区间讨论(零点分段法)
主题思想:分类讨论 零点分区间: 例如零点为:x+5=0或 x-3=0 的话x=-5 或x=3即为零点
当x≤-5,-x-5-(-x+3)>10 即-8>10,不成立
当-5≤x<3 即2x>8,解得x>4,不成立
当x≥3,x+5-(x-3)>10 即8>10,不成立
所以,不等式解集为空集
以上就是零点分段的大致过程与思想
对函数求解y=|a+1|中取出代数式求出零点a+1=0并求出零点a=-1.在数轴上表示a=-1.并分类讨论当a在数轴左(a<-1)和a在数轴右.(a>-1).并将两种代入y=|a+1|中.判断代数式的正负.并去掉绝对值符号.便化简完成求出分段函数,便化简完成。
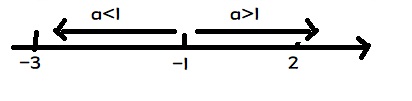
该解题过程如无其他要求,直接化简即可为.
解:原函数可化为
y={-a-1,a+1}
图像如图:

对含有绝对值的不等式求解:
对含有绝对值的不等式求解有两种
主要方法.一种是零点分段法,另一种是几何法,其中零点分段法其实上个化简数求解已述其模型,这里只做简单的例题解析.
零点分段法求解
解不等式|x+2|+|x-3|<7.
步骤一①找出区间范围.
由x+2=0 x-3=0得
x=-2 x=3.
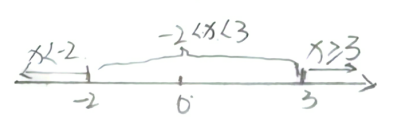
②区间论讨: x<-2 ,
(1)当x<-2时. 是
-(x+2)-(x-3)<7.
解得x>-3
结合x<-2故3<x<-2
(2)当-2<x<3时
x+2-x+3<7.
解得5<7恒成立满足所有实数
结合-2<x<3即解为-2<x<3.
(3)当x≥3时
.x+2+x-3<7.
解得x<4.结合x≥3得
原不等式解为 3<x<4.
综上三种情况
故解为-3<x<4.
几何分段法求解
解决上个例题当然有另一方式,即几何分段法
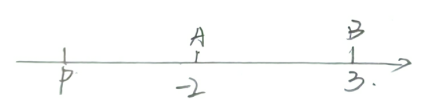
如图,先画一个数轴.令-2点为A.3点为B.假设P在A的左侧,此时(其中P表示为x)在.x+21+1x-31<7中.其中x+2表示x与(-2)的距离(因.x+2=0,即x=-2).x-3表示x与3的距离(原因同上).
这样1x+21+1x-31人7可转换为|PAI+1PB1<7.
①当P点处在A点左侧时
∴|PA|+|PBI其中|PB|=|PAI+|ABI.
|PA|+|PB|=|PA|+IPAI+|AB|<7且IABI=5
∴2|PAI+5<7.∴IPAI<1
因为P在左侧且PA间距离小于1所以点P处在3<P<之间.即3<x
②当点P处在A.B之间.
|PA|+|PBI<7可化为
|PA|+|PB|=|AB|=5<7恒成立
故点P在-2与3之间
即-2<x<3.
③当点P处在B点右侧
|PAI+|PB|<7可化为
且|PA|=|PBI+|AB|
即|PA|+|PB|=|PB|+|PB|+|AB|<7
∴2|PB|+5<7∴IPBI<1
因为D在B的右侧且处小于1个单位·∴P处在3<P<4即x<4.
综上三种情况解为-3人x<4.
这就是初中与高中的绝对值问题衔接,本篇拙作如有哪里写的有错误,还望各位斧正,感激不尽!



