[C++高性能计算]-牛顿冷却定律模拟物理冷却过程
最近学习NVIDIA官方的CUDA并行计算课程,有一个很好的例子,便跟着讲解,实现了一下,即一个物体(object)随着时间逐渐冷却的模拟过程,直接使用牛顿冷却定量进行模拟,一个对象进行计算,我们使用CPU单线程即可,后续我们尝试在大规模(>100M)数量的对象,进行CUDA加速计算。
原理
给定环境温度,求出物体当前温度与环境温度的差值,与比例系数K相乘,便能得到下一个阶段的温度。
dT(t) / dt=−k [T(t) − Tambient]我们采用欧拉法离散化微分式得到:
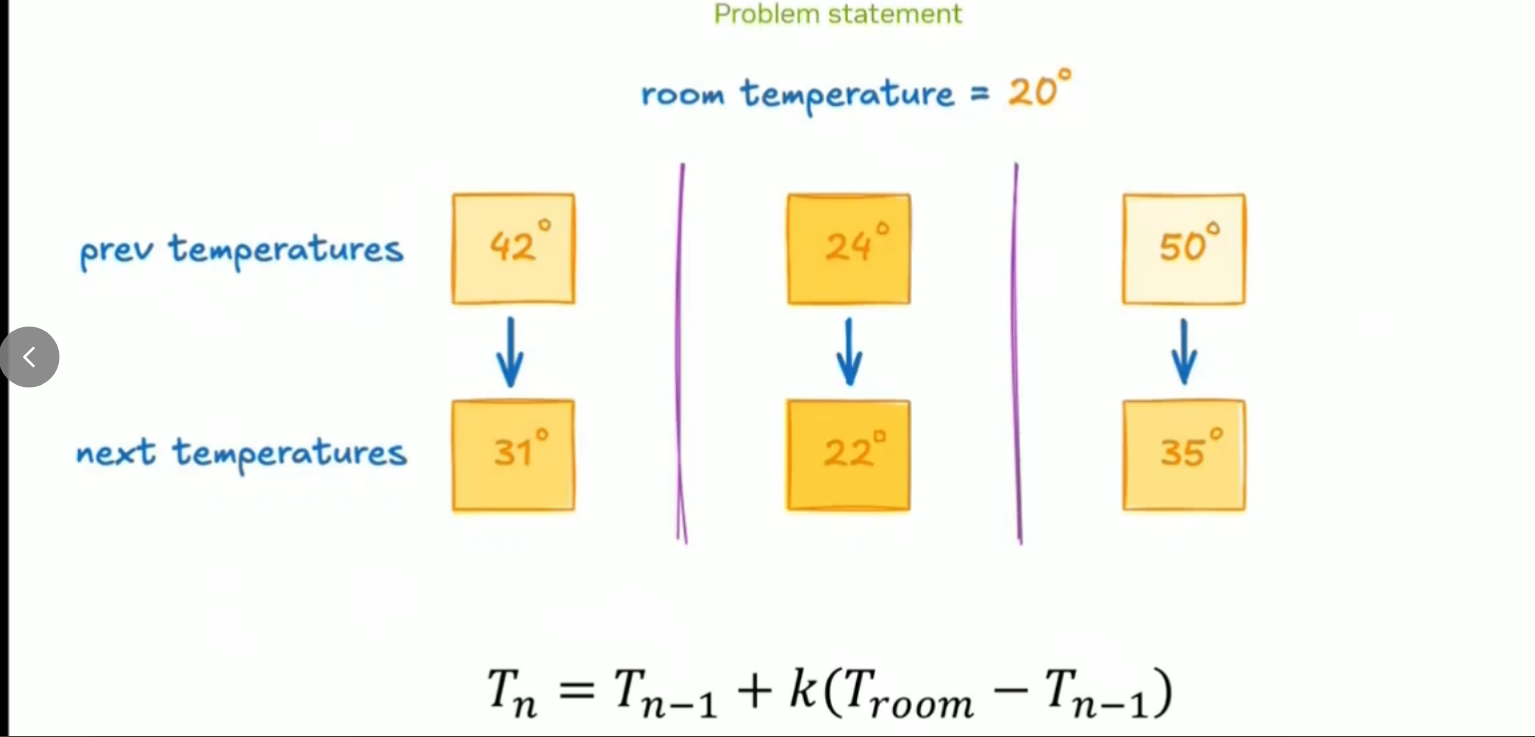
Tnew=Tcurrent+k⋅(Tambient−Tcurrent)假定环境温度20,目前三个对象分别温度对应42摄氏度,24摄氏度,50摄氏度,采用系数K=0.5的迭代系数。如表格,为三次时间迭代的温度结果。
| 时间步 | 计算过程 | 结果 |
|---|---|---|
T_0 | 初始值 | 42.0 |
T_1 | 42 + 0.5 \times (20 - 42) = 42 - 11 | 31.0 |
T_2 | 31 + 0.5 \times (20 - 31) = 31 - 5.5 | 25.5 |
定义参数变量
float k = 0.5; // 冷却系数
float ambient_temp = 20; // 环境温度
std::vector<float> temp(42, 24, 50); // 初始化三个物体的温度数学原理的Lambda函数
为了获所有外部变量(k和ambient_temp),我们需要加上 [=],最终实现每次调用计算一个物体下一步的温度。
auto op = [=](float temp) {
float diff = ambient_temp - temp;
return temp + k * diff;
};C++中Lambda函数是一个闭包函数,我们定义了一个op的lambda函数,[=]表示按值捕获外部所有变量,即我们在闭包函数内能够引用外部任何一个定义的变量。具体的lambda底层原理我们后续再讨论,我们用汇编代码演示具体lambda函数式怎么实现的。
迭代冷却过程
for (int step = 0; step < 3; step++) {
print(step, temp); // 打印当前状态
std::transform(temp.begin(), temp.end(), temp.begin(), op);
}我们进行三部冷却,其中计算部分我们调用了std : : transform()函数,这个函数的具体逻辑如下:
std::transform(temp.begin(), // 输入起始
temp.end(), // 输入结束
temp.begin(), // 输出起始(原地修改)
op); // 转换函数我们将transform函数是将temp向量中的每个元素,传入op这个lambda函数,op返回输出结果,输出结果同样传入到temp向量。更详细的说,temp.begin()返回一个迭代器,其实本质即temp向量的首个元素的泛化指针,即从temp中遍历所有元素,传入op匿名函数中,op返回的结果,逐个传入到temp.begin为初始地址的容器中去,这里即temp向量。
模拟结果
三个物体,分别是42℃,24℃,50℃的结果。
| 时间步 | 物体1温度(°C) | 物体2温度(°C) | 物体3温度(°C) | 备注 |
|---|---|---|---|---|
| 0 | 42.0 | 24.0 | 50.0 | 初始温度 |
| 1 | 31.0 | 22.0 | 35.0 | 第1次冷却后 |
| 2 | 25.5 | 21.0 | 27.5 | 第2次冷却后 |
尽管,少量物体进行计算模拟,性能不需要考虑,我们后续进行大规模模拟,我们进而探讨C++高性能计算的实现。
完整代码
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
float k = 0.5;
float ambient_temp = 20;
std::vector<float> temp = {42.0, 24.0, 50.0};
auto op = [=](float temp_val) {
return temp_val + k * (ambient_temp - temp_val);
};
std::cout << "步数 | 温度[0] | 温度[1] | 温度[2]" << std::endl;
std::cout << "----------------------------------" << std::endl;
for (int step = 0; step < 3; step++) {
std::cout << step << " | ";
for (float t : temp) {
std::cout << t << " ";
}
std::cout << std::endl;
std::transform(temp.begin(), temp.end(), temp.begin(), op);
}
return 0;
}



